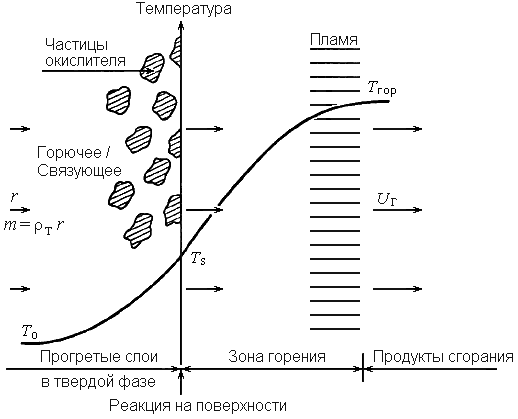
Рис. 34. Упрощенная модель горения СТТ
3.5.1. ДОПУЩЕНИЯ
Ниже выведены основные уравнения, используемые в большинстве моделей горения, и рассчитаны некоторые характеристики процесса [64, 178]. При этом сделаны следующие допущения.
Рис. 34 иллюстрирует эту упрощенную модель.

3.5.2. УРАВНЕНИЯ СОХРАНЕНИЯ В ТВЕРДОЙ ФАЗЕ
Для упрощения анализа сделаем еще три допущения:
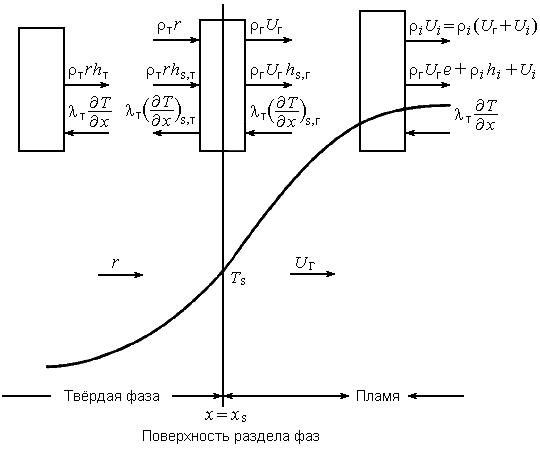
Поскольку давление в твердой фазе распределено равномерно, процесс описывается уравнением сохранения энергии (рис. 35)
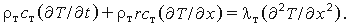 | (3.21a) |
Как правило, скорость горения r изменяется во времени, поэтому уравнение (3.21а) следует решать численно. Такая ситуация характерна для быстрых изменений r, например при воспламенении, погасании или вибрационном горении. Для стационарного горения получаем уравнение
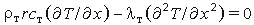 | (3.21б) |
с граничными условиями T = Ts при х=0 и T = T0 при х = -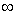 .
.
Однократное интегрирование дает
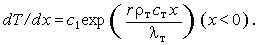 | (3.22) |
После второго интегрирования имеем
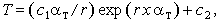 | (3.23) |
где 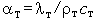 - коэффициент температуропроводности. Воспользовавшись граничными условиями, получим
- коэффициент температуропроводности. Воспользовавшись граничными условиями, получим
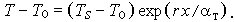 | (3.24) |
3.5.3. УСЛОВИЯ НА ПОВЕРХНОСТИ РАЗДЕЛА ТВЕРДАЯ ФАЗА-ГАЗ
Для твердой фазы скорость горения равна r при х = -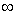 (рис. 35), и, согласно допущению (7), она постоянна вплоть до поверхности горения. Уравнения неразрывности и энергии на поверхности раздела имеют вид
(рис. 35), и, согласно допущению (7), она постоянна вплоть до поверхности горения. Уравнения неразрывности и энергии на поверхности раздела имеют вид
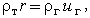 | (3.25) |
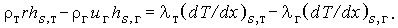 | (3.26) |
Энтальпии в уравнении энергии включают тепловой эффект реакции и скрытую теплоту фазового перехода. Обозначив последнюю величину Ls = hs,r - hsт и считая ее постоянной, получим для стационарных условий:
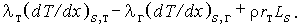 | (3.27) |
Если горение неустойчиво, то следует использовать другой подход [33].
3.5.4. УРАВНЕНИЯ СОХРАНЕНИЯ В ГАЗОВОЙ ФАЗЕ
Возвращаясь к рис. 35, запишем уравнения неразрывности и сохранения компонент:
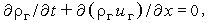 | (3.28) |
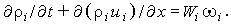 | (3.29а) |
Здесь 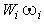 - скорость образования i-й компоненты в химической реакции. Вводя массовую долю
- скорость образования i-й компоненты в химической реакции. Вводя массовую долю 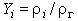 , получим
, получим
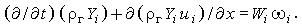 | (3.29б) |
Скорость i-й компоненты ui можно записать в виде суммы средней скорости газа uг и скорости диффузии i-й компоненты Ui, относительно средней скорости: ui = uг +Ui. Используя это определение, получим
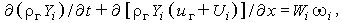 | (3.29в) |
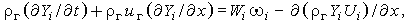 | (3.29г) |
так как по (3.28) 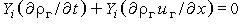 . Если предположить, что выполняется закон Фика и, более того, что все компоненты имеют одинаковые коэффициенты диффузии D, т. е.
. Если предположить, что выполняется закон Фика и, более того, что все компоненты имеют одинаковые коэффициенты диффузии D, т. е.
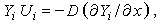 | (3.30) |
то получим уравнение сохранения для i-й компоненты в окончательном виде:
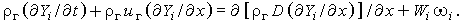 | (3.31) |
Обозначая через е полную внутреннюю энергию (тепловую и кинетическую), включая работу puг, совершаемую силами давления, и учитывая, что каждая компонента переносит свою энтальпию со скоростью 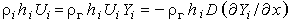 [последнее равенство следует из (3.30) ], запишем уравнение сохранения энергии в виде
[последнее равенство следует из (3.30) ], запишем уравнение сохранения энергии в виде
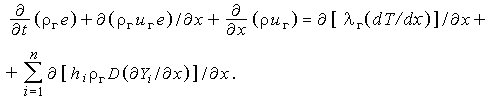 | (3.32а) |
Поскольку 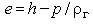 , возможна альтернативная запись:
, возможна альтернативная запись:
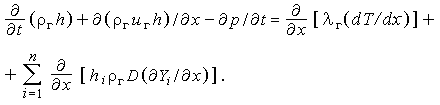 | (3.32б) |
Используя (3.28), последнее уравнение можно переписать в виде
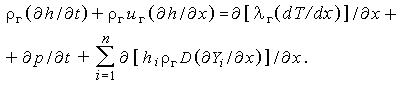 | (3.32в) |
Теперь, положив 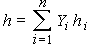 , получим для левой части уравнения:
, получим для левой части уравнения:
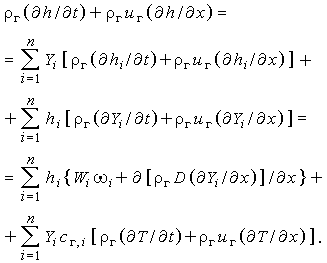 | (3.32г) |
Здесь использовано уравнение (3.31) и соотношение
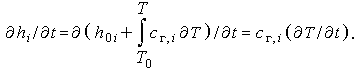 |
Полагая cг i = const и учитывая, что теплоемкость газа определяется как 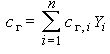 , а
, а 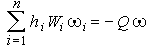 , где Q - тепловой эффект, а
, где Q - тепловой эффект, а 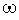 - скорость реакции, получим для правой части:
- скорость реакции, получим для правой части:
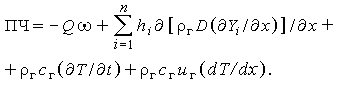 | (3.32д) |
Из (3.32в,д) окончательно имеем
 | (3.33а) |
Предположив, что все газы имеют одинаковую теплоемкость, это уравнение можно упростить, так как
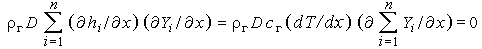 |
и, следовательно,
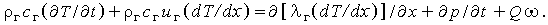 | (3.33б) |
Для стационарного течения последнее уравнение принимает вид
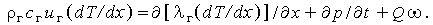 | (3.33в) |
Это уравнение можно решить,
если предположить, что химическая реакция протекает в очень узком слое на
расстоянии х = х* от поверхности раздела
твёрдой и газовой фаз, т. е. 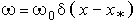 ,
где
,
где 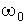 = const, а
= const, а 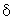 - функция,
как обычно, удовлетворяет условию
- функция,
как обычно, удовлетворяет условию 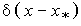 = 0 при 0<х<х* и
= 0 при 0<х<х* и
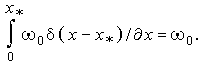 |
Таким образом, для 0<x<x* получаем уравнение
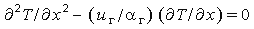 | (3.34) |
которое при граничных условиях T = Ts и dT / dx = (dT / dx)s,г при х + 0 имеет решение
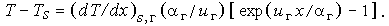 | (3.35a) |
При х = х* имеем T = Tгор и, следовательно,
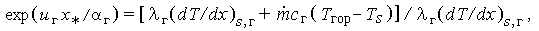 | (3.35б) |
где 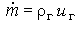 -поток массы. Поскольку тепловой эффект реакции удовлетворяет соотношению
-поток массы. Поскольку тепловой эффект реакции удовлетворяет соотношению
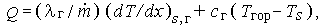 |
то
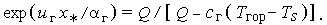 | (3.35в) |
С другой стороны, тепло, поступающее на поверхность раздела, определяется выражением
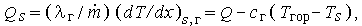 |
так что расстояние от поверхности до фронта пламени х* можно рассчитать по формуле
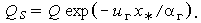 | (3.36) |
3.5.5. ХАРАКТЕРИСТИЧЕСКИЕ ПАРАМЕТРЫ ПРОЦЕССА ГОРЕНИЯ
Теперь, используя константы и физико-химические свойства ТРТ, приведенные в табл. 6, рассчитаем значения некоторых характеристических параметров зоны горения.
Таблица 6. Физико-химические свойства типичного ТРТ [64]
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Предположим, что при горении ТРТ устанавливается температурный профиль, показанный на рис. 36. Если не включать в рассмотрение теплоту фазового превращения в объеме твердой фазы, то тепловой поток на твердую поверхность определяется соотношениями
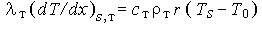 со стороны твердой фазы,
со стороны твердой фазы,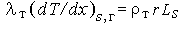 со стороны газа,
со стороны газа,
где Ls следует рассматривать как "тепловой эффект" эндотермической реакции газификации на поверхности топлива.
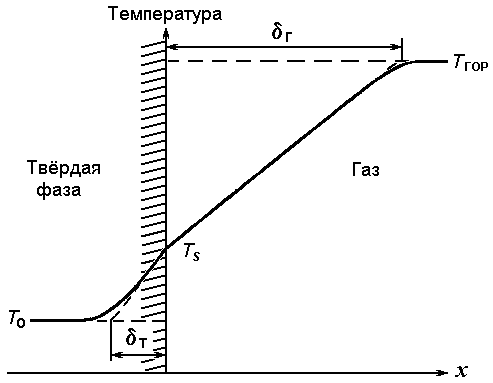 |
| Рис. 36. Принятый профиль температуры [64]. |
Используя определение толщин тепловых слоев в твердой фазе
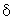 т и в газе
т и в газе 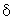 г,
приведенные на рис. 36, получим
г,
приведенные на рис. 36, получим
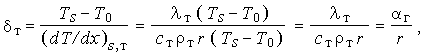 | (3.37) | |
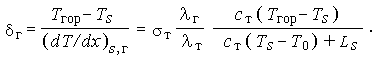 |
Подставляя величины из табл. 6, получим для толщины
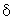 т прогрева твердой фазы в тепловой
волне значение 19,1 мкм при TS=900К. Используя измеренное
Саммерфилдом значение
т прогрева твердой фазы в тепловой
волне значение 19,1 мкм при TS=900К. Используя измеренное
Саммерфилдом значение 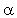 т = 1,935*10-7 м2*c-1
и полагая r = 10-2 м2*c-1,
получим
т = 1,935*10-7 м2*c-1
и полагая r = 10-2 м2*c-1,
получим  т = 19,35 мкм,
что хорошо согласуется с расчетом. Для газовой фазы рассмотрим три случая: когда существует теплоотвод интенсивностью 100 кал*г-1, теплоподвод интенсивностью 100кал*г-1 и когда поверхностная реакция отсутствует. Результаты расчетов приведены в табл. 7 и показаны графически на рис. 37. По ним можно сделать следующее заключение: расстояние от поверхности до фронта пламени в газовой фазе и толщина прогретого слоя в твердой фазе при рассматриваемых давлениях (около 5 МПа) имеют порядок 20 мкм.
т = 19,35 мкм,
что хорошо согласуется с расчетом. Для газовой фазы рассмотрим три случая: когда существует теплоотвод интенсивностью 100 кал*г-1, теплоподвод интенсивностью 100кал*г-1 и когда поверхностная реакция отсутствует. Результаты расчетов приведены в табл. 7 и показаны графически на рис. 37. По ним можно сделать следующее заключение: расстояние от поверхности до фронта пламени в газовой фазе и толщина прогретого слоя в твердой фазе при рассматриваемых давлениях (около 5 МПа) имеют порядок 20 мкм.
|
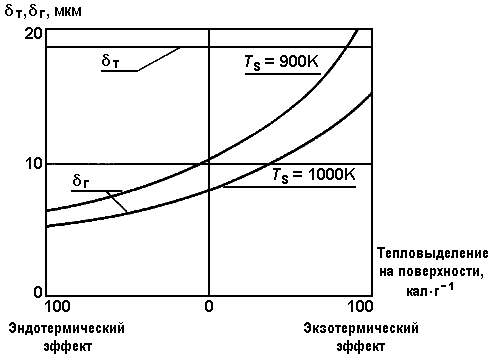 |
| Рис. 37. Характерные параметры зоны горения [64]. |
Теперь проверим справедливость допущения (7) относительно гомогенности топлива. Типичные значения диаметра частиц окислителя в СТТ составляют от 5 до нескольких сотен мкм. Характерная длина в температурном профиле твердой фазы равна
 т / r ~ 20 мкм. Следовательно, предположение о гомогенности твердой фазы оправданно лишь при Dок << 20 мкм.
Поскольку размеры частиц окислителя, как правило, одного порядка с указанной
характерной длиной (или даже больше ее), то приходится сделать вывод, что
модель, основанная на допущении (7), позволяет прогнозировать лишь тенденции
изменения скорости горения. Для учета гетерогенной структуры топлива в модель
следует добавить по крайней мере процедуру статистического осреднения. В общем
случае величины
т / r ~ 20 мкм. Следовательно, предположение о гомогенности твердой фазы оправданно лишь при Dок << 20 мкм.
Поскольку размеры частиц окислителя, как правило, одного порядка с указанной
характерной длиной (или даже больше ее), то приходится сделать вывод, что
модель, основанная на допущении (7), позволяет прогнозировать лишь тенденции
изменения скорости горения. Для учета гетерогенной структуры топлива в модель
следует добавить по крайней мере процедуру статистического осреднения. В общем
случае величины  т и
т и
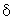 г будут существенно меняться в
зависимости от давления, температуры поверхности и энерговыделения на
поверхности.
г будут существенно меняться в
зависимости от давления, температуры поверхности и энерговыделения на
поверхности.